English

• 1. INTRODUCTION

  The experimentally available graphene has ignited great scientific interest on two-dimensional (2D) materials for use in the next generation high-speed nanoelectronic devices owing to their exotic electronic, optical and catalytic properties^[1-3]. The 2D materials with excellent performances like silicene^[4-8], germanene^{[9, 10]}, phosphorene^{[11, 12]}, transition metal dichalcogenides (TMDs)^{[13, 14]} and transition metal carbides/nitrides (MXenes)^[15-17] have been synthesized and intensively explored. Among them, silicene has a buckled honeycomb lattice similar to graphene but with a host of exotic electronic properties^[7]. Compared with graphene, silicene has several prominent advantages, such as a much stronger spin-orbital coupling, a better tunability of band gap and an easier valley polarization^[8]. Furthermore, monolayer silicene was successfully synthesized on various substrates, including Ag (111)^[18], Ir (111)^{[19, 20]}, ZrC (111)^[21] and ZrB₂^[22] surfaces. Tremendous efforts have been devoted to exploring the intrinsic properties as well as potential applications for monolayer silicene and its derivatives, such as chemical sensor^[23-25], field effect transisitor (FET)^[26-28], thermoelectric device^{[29, 30]}, hydrogen storage^[31-33] and electrode materials for Li battery^{[34, 35]}.

  Inspired by the experimental realization of silicene, 2D silicide monolayers and few-layers materials have attracted increasing research attention for their distinctive properties^[36-42]. For instance, unusual chemical bonding in quasi-planar Ni₂Si free-standing 2D monolayer has been revealed, which shows higher stability than silicene and germanene^[39]. In addition, 2D Fe₂Si nanosheet has been theretically predicted as a ferromagnetic half metal with enhanced spin-polarization ratio, and the 2D structure and strong in-plane Fe–Fe interaction endow Fe₂Si nanosheet magnetocrystalline anisotropy energy with the magnitude of at least two orders larger than those of Fe, Co and Ni bulks, with great potential for spintronic nanodevices^[41]. Moreover, a novel stable planar hexacoordinate 2D Cu₂Si monolayer has been designed with strong chemical bonding and high inplane stiffness, which is the global minimum stucture in the 2D space^[37]. Excitedly, two-dimensional Dirac nodal line fermions in monolayer Cu₂Si have been experimentally realized, which provides opportunities to realize high-speed low-dissipation devices^[40]. Therefore, exploring experimentally feasible 2D silicide nanosheet and the potential performances in nanoelectronics are of great interest and importance.

  Moreover, 2D materials with planar hyper-coordinate motifs are extremely rare due to the difficulty in stabilizing the planar hyper-coordinate configurations in extended systems^{[37, 43]}. It is challenging to create 2D planar hypercoordinate materials, which needs to match the constituent elements both geometrically and electronically. It is interesting to note that the transition metal related silicides prefer being in close-packed atomic configuration with hexa-coordination in 2D space, such as 2D Cu₂Si, Ni₂Si and Fe₂Si monolayers just mentioned, which is contrary to the honeycomb structure of prototypical graphene with tricoordination. Then it is natural to wonder if there is any other stable 2D silicide featuring this planar hyper-coordinate structure with novel electronic properties besides these 2D transition metal related silicides.

  Interestingly, recently an infinite CaSi monolayer^[42] with quasi-planar pentacoordinate silicon has been explored theoretically on the condition that the bonding pattern of planar penta-coordinate silicon species of Ca₄Si₂^2- is discovered. It shows that CaSi monolayer is a natural semiconductor with an indirect band gap of 0.5 eV, which has rather strong optical absorption in the visible region of solar spectrum. On the other hand, Ca₂Si as one of the typical alkaline earth metal (AEM) silicide with semiconductor character has gained attentions for its potential applications in thermoelectrics and optoelectronics^{[44, 45]}. However, to the best of our knowledge, there is no report on the stability of 2D Ca₂Si nanosheet and its electronic properties until now.

  In this work, by means of ab initio evolutionary algorithm calculations, we predict a novel 2D Ca₂Si monolayer with quasi-planar hexa-coordinate structure. Our calculations demonstrate that the Ca₂Si monolayer is an indirect semiconductor with the band gap of about 0.77 eV, which is thermally and dynamically stable for experimental synthesis. It is interesting that the Ca₂Si monolayer exhibits high electron carrier mobility with strong directionally anisotropic character, which could effectively facilitate the migration and separation of the electron-hole pairs for nano-electronic devices.

  2. COMPUTATIONAL METHODS

  The calculations were based on density functional theory (DFT) implemented in the Vienna ab initio simulation package (VASP)^[46–49] in conjunction with the projector augmented wave (PAW) pseudopotentials^{[49, 50]}. The generalized gradient approximation (GGA)^[51] of Perdew-Burke-Ernzerhof (PBE)^[52] was used for the exchange correlation interactions between electrons^{[52, 53]}. The cutoff energy was set to 500 eV, which was sufficient to accurately describe the outer valence electrons of Ca: 3s²3p⁶4s² and Si: 3s²3p². The convergence criteria for energy and force were set to 10^-5 eV⋅atom^-1 and 0.02 eV⋅Å^-1, respectively, and the lattice constant was optimized using the same method. We maintained a sufficiently large vacuum space (20 Å vacuum layer) in a direction perpendicular to the plane of the plate to ensure that there was no significant interaction between the two adjacent layers. In geometric optimization and static self-consistent calculations, k-sampling was performed using 13 × 13 × 1 points by the Monkhorst-Pack^[54] k meshes for structural optimization and electronic structure calculation. Compared with the band gap with underestimated PBE functional, the HSE06 hybrid density functional^[55] was used to precisely evaluate the electronic band structure of Ca₂Si monolayer.

  The electron localization function (ELF)^{[56, 57]} was calculated from the VASP electronic densities:

  $ {\text{ELF}} = \frac{1}{{1 + \frac{{20\sum\limits_i {{{\left| {\nabla {\varphi _i}} \right|}^2} - 5\frac{{{{\left| {\nabla \rho } \right|}^2}}}{\rho }} }}{{12{{(3{{\text{π }}^2})}^{\frac{5}{3}}}{\rho ^{\frac{5}{3}}}}}}} $

  (1)

  where ${\varphi _{\text{i}}}$ is the single determinant wave function from Hartree Fock or Kohn Sham orbitals, and $\rho $ is the charge density. The crystal orbital Hamiton population (COHP) analyses were performed based on the LOBSTER code^[58]. The phonon dispersion calculation was performed using the super-cell finite displacement method implemented in the YPHON software package^[59], and the k-point sampling grid was used to evaluate the force of the 3 × 3 × 1 super unit. In addition, Born-Oppenheimer ab initio molecular dynamics (AIMD) simulations were employed to study the thermal stability of Ca₂Si monolayer, for which a 6 × 6 × 1 supercell and 10 ps with each time step of 1 fs from 300 to 1500 K were considered.

  For 2D intrinsic inorganic semiconductor, the carrier mobility is mainly dominated by the phonon scattering, which can be described by the deformation potential theory. Therefore, the carrier mobility of Ca₂Si monolayer was studied based on the deformation potential theory with the following analytical expression^[60–62]:

  $ {\mu _{2{\text{D}}}} = 2\frac{{2e{\hbar ^{\text{3}}}{C_{2{\text{D}}}}}}{{3{k_{\text{B}}}T{{\left| {{m^*}} \right|}^2}{E_i}^2}} $

  (2)

  where $ e $ is the electron charge, $ \hbar $the reduced Planck constant, $ {k_{\text{B}}} $the Boltzmann constant and $ T $ the temperature (300 K), while $ {m^*} $, $ {E_i} $ and $ {C_{2{\text{D}}}} $ are the effective mass, deformation potential constant of the carrier, and elastic modulus under the uniaxial strain along the transport direction, respectively.

  3. RESULTS AND DISCUSSION

  By means of the ab initio evolutionary algorithm calculations, we have obtained the novel 2D Ca₂Si monolayer with a = 4.694 Å. The optimized structure of the symmetric Ca₂Si monolayer exhibits a quasi-planar 2D hexa-coordinated structure with each Si atom coordinated by six Ca atoms (hexa-coordinate silicon) and each Ca coordinated by three Si and three Ca atoms (hexa-coordinate calcium), as illustrasted in Fig. 1a. The structure is the first example in hexa-coordinated AEM silicide, which is similar to the quasi-planar 2D Ni₂Si^[39] and Fe₂Si^[41] monolayers.

  Figure 1

  

  Figure 1.  (a) Side and top views of the optimized structure of 2D Ca₂Si monolayer. (b) ELF profile on the (110) plane of Ca₂Si monolayer. The interval between the contour lines is 0.16. (c) The calculated COHP of Ca–Si and Ca–Ca bonds in Ca₂Si monolayer. The inset of Fig. 1c is the 3D ELF profile of Ca₂Si monolayer

  DownLoad: Full-Size Img PowerPoint

  To understand the chemical bonding interaction, we introduced electron localization function (ELF) analyses for Ca₂Si monolayer. The ELF contour plots on the (110) plane of Ca₂Si monolayer using PBE are displayed in Fig. 1b. It shows that the ELF value at Ca and Si atom sites is very small, while there is strong electron localization around the Ca–Si bonds with the ELF value of about 0.86, illustrating strong covalent bonding states with localized electron character in the Ca₂Si monolayer. On the other hand, the weak localized electrons between two Ca atoms indicate the two neighbored Ca atoms are weakly bonded. To further explore the Ca–Si and Ca–Ca bonding interactions in Ca₂Si monolayer, we performed the crystal orbital Hamilton population (COHP) to describe the energy resolved chemical bonding character by presenting the delocalized electronic structure in real space^[63]. Fig. 1c displays the calculated COHP of Ca–Si and Ca–Ca bonds in Ca₂Si monolayer, where the bonding interaction exhibits a negative Hamiltonian off-site element and the antibonding interaction is characterized by a positive one^[64]. It should be noted that no antibonding states occupied the Fermi level, suggesting chemical bonding interactions are stable for Ca₂Si monolayer. Additionally, Ca₂Si monolayer exhibits a typical semiconductor with the band gap of about 0.37 eV from the interactions of Ca–Si and Ca–Ca bonds in Fig. 1c. The three-dimensional (3D) ELF profile of Ca₂Si monolayer also exhibits strong electron localization around the Ca–Si bond, as shown in the inset of Fig. 1c.

  To verify the stability of Ca₂Si monolayer at ambient condition, we employed ab initio molecular dynamics (AIMD) simulations and phonon dispersion curves to evaluate the thermal and lattice dynamical stabilities. The evolution of the total energy and structure snapshots performed by AIMD simulations is illustrated in Fig. 2a~2e. After annealing from 300 to 1200 K for 10 ps, the evolution of the total energy oscillates only over a very narrow range and the atoms well maintain with slight vibration around their equilibrium positions in the network structure, keeping quasiplanar hexa-coordinate motifs. However, after annealing up to 1500 K for 10 ps, the crystal structure of Ca₂Si monolayer is seriously disrupted with atoms deviating significantly from their equilibrium positions and the chemical bonds broken. The results reveal that the Ca₂Si monolayer has very good thermal stability and can maintain its structural integrity up to 1200 K. Furthermore, we calculated the phonon dispersion curves to explore the lattice stability of Ca₂Si monolayer under ambient condition, as displayed in Fig. 2f. Ca₂Si monolayer exhibits good lattice dynamical stability without any negative or imaginary frequency, indicating that the Ca₂Si monolayer could be lattice dynamically stable. Considering the rapid development of experimental techniques for low-dimensional materials in recent years, we are optimistic that the Ca₂Si monolayer can be synthesized in future.

  Figure 2

  

  Figure 2.  Evolution of total energy and snapshots from AIMD simulations at 0 and 10 ps at (a) 300 K, (b) 600 K, (c) 900 K, (d) 1200 K and (e) 1500 K of Ca₂Si monolayer. (f) Phonon dispersion curve of Ca₂Si monolayer under ambient condition using PBE functional

  DownLoad: Full-Size Img PowerPoint

  To get insight into electronic properties, the projected energy band structure of Ca₂Si monolayer was respectively calculated by GGA-PBE and HSE06 hybrid functional methods, as plotted in Figs. 3a and 3b. It shows that Ca₂Si monolayer exhibits indirect semiconductor behavior with band gap about 0.36 eV by GGA-PBE method, but with relatively larger band gap about 0.77 eV using the HSE06 method. It can be understood easily that the PBE calculation often appropriately underestimates the value of band gap. Note that both PBE and HSE06 results exhibit similar band dispersion curves for Ca₂Si monolayer, with the conduction band minimum (CBM) located at G point and the valence band maximum (VBM) occupied at the M point. Moreover, the conductive band of Ca₂Si monolayer is contributed by Si electrons, while the valence band near Fermi level is mainly occupied by Ca electrons.

  Figure 3

  

  Figure 3.  Projected energy band structure of Ca₂Si monolayer by (a) GGA–PBE and (b) HSE06 hybrid functional methods. The red and blue solid lines represent the projected specific gravity of Si electrons and Ca electrons, respectively. The fermi level is set to E = 0.0 eV

  DownLoad: Full-Size Img PowerPoint

  The electronic properties of 2D materials are mainly determined by the carrier mobility (μ), which is greatly influenced by their effective masses^[65]. Herein, we studied the carrier mobility of Ca₂Si monolayer to explore the mechanism of migration and separation of the generated electron-hole pairs along zigzag (x) and armchair (y) directions. Here we used an orthorhombic lattice to calculate the intrinsic responses of Ca₂Si monolayer under uniaxial strain. The orthorhombic structure, transformed Brillouin zone as well as band structure of Ca₂Si monolayer are displayed in Fig. 4a–b. The band nature of CBM or VBM occupying the Г point implies the effective mass (m^*) of carriers, and usually a stronger dispersion of the band indicates a smaller m^* for carriers. To obtain the elastic modulus C_2D and deformation potential constant E_i, we respectively calculated the total energy shift E – E₀ and band edge positions as a function of the uniaxial strain ε along x and y directions by PBE, as shown in Fig. 4c–d. The calculated m^*⋅m₀^–1, C_2D, E_i and μ for Ca₂Si monolayer are summarized in Table 1. The effective masses of Ca₂Si monolayer are 1.064 m₀ (0.986 m₀) for electrons and 1.105 m₀ (28.902 m₀) for holes along x (y) direction, respectively. The predicted carrier mobility of electrons is 4590.47 cm²⋅V^–1⋅s^–1 along the y direction, which is larger than that along the x direction (1894.92 cm²⋅V^–1⋅s^–1). On the contrary, the carrier mobility of holes along the x direction is larger than that along y (22.13 vs. 0.24 cm²⋅V^–1⋅s^–1). The results illustrate that Ca₂Si monolayer exhibits a very high directionally anisotropic transport character for electrons and holes.

  Figure 4

  

  Figure 4.  (a) Using an orthorhombic lattice instead of a traditional hexagonal lattice to calculate Ca₂Si monolayer and the transformed Ca₂Si monolayer Brillouin zone. (b) Band structure of Ca₂Si monolayer by PBE. (c) Total energy shift E – E₀ and (d) Band edge positions of Ca₂Si monolayer as a function of the uniaxial strain ε along both the zigzag (x) and armchair (y) directions by PBE. The vacuum level is set to 0 for reference in (d) figure

  DownLoad: Full-Size Img PowerPoint

  Table 1

  

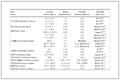  Table 1.  Calculated Effective Mass (m*), Elastic Modulus C_2D, Deformation Potential Constant E_i, and Carrier Mobilityμ for Electrons and Holes along Both the Zigzag (x) and Armchair (y) Directions at 300 K in Ca₂Si Monolayer

  DownLoad: CSV

  Carrier type	m*·m0–1	C2D (N·m–1)	|Ei| (eV)	μ (cm2·V–1·s–1)
  Electron (x)	1.064	31.99	0.465	1894.92
  Hole (x)	1.105	31.99	4.144	22.13
  Electron (y)	0.986	31.92	0.322	4590.47
  Hole (y)	28.902	31.92	1.518	0.24

  To visualize the anisotropy of carrier mobility for Ca₂Si monolayer, the carrier mobility of electrons and holes as a function of directions is plotted in Fig. 5. It is obvious that the electron mobility along y direction is twice larger than that along x, while the hole mobility along the x direction is nearly 91 times larger than that along y. The results indicate that the carrier mobility of Ca₂Si monolayer is directionally anisotropic, where the electrons mainly migrate along y direction and the holes tend to absolutely migrate along x direction, leading to the effective separation of electron-hole pairs. Moreover, it is worth noting that the electrons mobility is significantly larger than that of the holes both along the x and y directions (more than 85 times larger), indicating that carrier mobility for Ca₂Si monolayer is electron-dominated, which is attributed by the relatively small effective mass and the deformation potential constant. The migration of electrons in Ca₂Si monolayer is competitive compared with the black phosphorous monolayer (from hundreds to thousands)^[65] and higher than that of single-layer MoS₂ (~200 cm²⋅V^–1⋅s^–1)^[66]. Therefore, the carrier mobility with strong directional anisotropy in Ca₂Si monolayer facilitates fast migration and efficient separation of the generated electron-hole pairs, indicating that Ca₂Si monolayer has great potential for high efficiency solar cells and other electronic applications. Moreover, this mechanism for the separation of electron-hole pairs can provide design principles to other low-dimensional semiconductors.

  Figure 5

  

  Figure 5.  Carrier mobility of electrons and holes as a function of directions for Ca₂Si monolayer

  DownLoad: Full-Size Img PowerPoint

  4. CONCLUSION

  In summary, we have predicted a new 2D Ca₂Si monolayer with quasi-planar hexa-coordinate structure based on first-principles calculations. The calculated COHP of Ca–Si and Ca–Ca bonds shows that the chemical bonding interactions are stable in Ca₂Si monolayer. Additionally, AIMD calculations and phonon dispersion curves exhibit that the Ca₂Si monolayer is thermally and dynamically stable. The HSE06 band structure analyses show that Ca₂Si monolayer is a semiconductor with indirect band gap about 0.77 eV. It is interesting that the calculated electron mobility along the y direction is larger than that along x (4590.47 vs. 1894.92 cm²⋅V^–1⋅s^–1), while the hole mobility along the x direction is larger than that along y (22.13 vs. 0.24 cm²⋅V^–1⋅s^–1). The results indicate strong directionally anisotropic carrier mobility in Ca₂Si monolayer, which could effectively facilitate the migration and separation of the generated electron-hole pairs. Our calculations demonstrate that the Ca₂Si monolayer could be a potential candidate for nano-electronic devices in future.

  
  
• 1. [1]

     Dinh, K. N.; Liang, Q.; Du, C. F.; Zhao, J.; Tok, A. I. Y.; Mao, H.; Yan, Q. Nanostructured metallic transition metal carbides, nitrides, phosphides, and borides for energy storage and conversion. Nano. Today 2019, 25, 99−121. doi: 10.1016/j.nantod.2019.02.008

  2. [2]

     Gupta, A.; Sakthivel, T.; Seal, S. Recent development in 2D materials beyond graphene. Prog. Mater. Sci. 2015, 73, 44−126. doi: 10.1016/j.pmatsci.2015.02.002

  3. [3]

     Mortazavi, B.; Dianat, A.; Cuniberti, G.; Rabczuk, T. Application of silicene, germanene and stanene for Na or Li ion storage: a theoretical investigation. Electrochim. Acta 2016, 213, 865−870. doi: 10.1016/j.electacta.2016.08.027

  4. [4]

     Oughaddou, H.; Enriquez, H.; Tchalala, M. R.; Yildirim, H.; Mayne, A. J.; Bendounan, A.; Dujardin, G.; Ait Ali, M.; Kara, A. Silicene, a promising new 2D material. Prog. Surf. Sci. 2015, 90, 46−83. doi: 10.1016/j.progsurf.2014.12.003

  5. [5]

     Zhuang, J.; Xu, X.; Feng, H.; Li, Z.; Wang, X.; Du, Y. Honeycomb silicon: a review of silicene. Sci. Bull. 2015, 60, 1551−1562. doi: 10.1007/s11434-015-0880-2

  6. [6]

     Ali, M.; Ni, Z.; Cottenier, S.; Liu, Y.; Pi, X.; Yang, D. Formation, structures and electronic properties of silicene oxides on Ag(111). J. Mater. Sci. Technol. 2016, 33, 751−757.

  7. [7]

     Zhao, J.; Liu, H.; Yu, Z.; Quhe, R.; Zhou, S.; Wang, Y.; Liu, C. C.; Zhong, H.; Han, N.; Lu, J.; Yao, Y.; Wu, K. Rise of silicene: a competitive 2D material. Prog. Mater. Sci. 2016, 83, 24−151. doi: 10.1016/j.pmatsci.2016.04.001

  8. [8]

     Molle, A.; Grazianetti, C.; Tao, L.; Taneja, D.; Alam, M. H.; Akinwande, D. Silicene, silicene derivatives, and their device applications. Chem. Soc. Rev. 2018, 47, 6370−6387. doi: 10.1039/C8CS00338F

  9. [9]

     Lee, J. H.; Lee, E. K.; Joo, W. J.; Jang, Y.; Kim, B. S.; Lim, J. Y.; Choi, S. H.; Ahn, S. J.; Ahn, J. R.; Park, M. H. Wafer-scale growth of single-crystal monolayer graphene on reusable hydrogen-terminated germanium. Science 2014, 344, 286−289. doi: 10.1126/science.1252268

  10. [10]

      Ni, Z.; Minamitani, E.; Ando, Y.; Watanabe, S. The electronic structure of quasi-free-standing germanene on monolayer MX (M = Ga, In; X = S, Se, Te). Phys. Chem. Chem. Phys. 2015, 17, 19039−19044. doi: 10.1039/C5CP02428E

  11. [11]

      Sa, B.; Li, Y. L.; Qi, J.; Ahuja, R.; Sun, Z. Strain engineering for phosphorene: the potential application as a photocatalyst. J. Phys. Chem. C 2014, 118, 26560−26568. doi: 10.1021/jp508618t

  12. [12]

      Li, L.; Yu, Y.; Ye, G. J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X. H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372−377. doi: 10.1038/nnano.2014.35

  13. [13]

      Wang, Q. H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J. N.; Strano, M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699−712. doi: 10.1038/nnano.2012.193

  14. [14]

      Peng, Q.; Wang, Z.; Sa, B.; Wu, B.; Sun, Z. Electronic structures and enhanced optical properties of blue phosphorene/transition metal dichalcogenides van der Waals heterostructures. Sci. Rep. 2016, 6, 31994−10. doi: 10.1038/srep31994

  15. [15]

      Guo, Z.; Zhou, J.; Zhu, L.; Sun, Z. MXene: a promising photocatalyst for water splitting. J. Mater. Chem. A 2016, 4, 11446−11452. doi: 10.1039/C6TA04414J

  16. [16]

      Naguib, M.; Mochalin, V. N.; Barsoum, M. W.; Gogotsi, Y. MXenes: a new family of two-dimensional materials. Adv. Mater. 2014, 26, 982−982. doi: 10.1002/adma.201470041

  17. [17]

      Rehman, G.; Khan, S. A.; Amin, B.; Ahmad, I.; Gan, L. Y.; Maqbool, M. Intriguing electronic structures and optical properties of two-dimensional van der Waals heterostructures of Zr₂CT₂ (T = O, F) with MoSe₂ and WSe₂. J. Mater. Chem. C 2018, 6, 2830−2839. doi: 10.1039/C7TC05963A

  18. [18]

      Sone, J.; Yamagami, T.; Aoki, Y.; Nakatsuji, K.; Hirayama, H. Epitaxial growth of silicene on ultra-thin Ag(111) films. New J. Phys. 2012, 16, 095004−15.

  19. [19]

      Meng, L.; Wang, Y.; Zhang, L.; Du, S.; Wu, R.; Li, L.; Zhang, Y.; Li, G.; Zhou, H.; Hofer, W. Buckled silicene formation on Ir(111). Nano. Lett. 2013, 13, 685−690. doi: 10.1021/nl304347w

  20. [20]

      Cherukara, M. J.; Narayanan, B.; Chan, H.; Skrs, S. Silicene growth through island migration and coalescence. Nanoscale 2017, 9, 10.1039. C1037NR03153J, 10186−10192.

  21. [21]

      Aizawa, T.; Suehara, S.; Otani, S. Silicene on zirconium carbide (111). J. Phys. Chem. C 2014, 118, 23049−23057. doi: 10.1021/jp505602c

  22. [22]

      Gill, T. G.; Fleurence, A.; Warner, B.; Prüser, H.; Friedlein, R.; Sadowski, J. T.; Hirjibehedin, C. F.; Yamadatakamura, Y. Metallic atomically-thin layered silicon epitaxially grown on silicene/ZrB₂. 2D Mater. 2017, 4, 021015−7. doi: 10.1088/2053-1583/aa5a80

  23. [23]

      Feng, J. W.; Liu, Y. J.; Wang, H. X.; Zhao, J. X.; Cai, Q. H.; Wang, X. Z. Gas adsorption on silicene: a theoretical study. Comp. Mater. Sci. 2014, 87, 218−226. doi: 10.1016/j.commatsci.2014.02.025

  24. [24]

      Wei, H.; Nan, X.; Xiaojun, W.; Zhenyu, L.; Jinlong, Y. Silicene as a highly sensitive molecule sensor for NH₃, NO and NO₂. Phys. Chem. Chem. Phys. 2014, 16, 6957−6962. doi: 10.1039/c3cp55250k

  25. [25]

      Chandiramouli, R.; Srivastava, A.; Nagarajan, V. NO adsorption studies on silicene nanosheet: DFT investigation. Appl. Surf. Sci. 2015, 351, 662−672. doi: 10.1016/j.apsusc.2015.05.166

  26. [26]

      Ni, Z.; Zhong, H.; Jiang, X.; Quhe, R.; Luo, G.; Wang, Y.; Ye, M.; Yang, J.; Shi, J.; Lu, J. Tunable band gap and doping type in silicene by surface adsorption: towards tunneling transistors. Nanoscale 2014, 6, 7609−7618. doi: 10.1039/C4NR00028E

  27. [27]

      Tao, L.; Cinquanta, E.; Chiappe, D.; Grazianetti, C.; Fanciulli, M.; Dubey, M.; Molle, A.; Akinwande, D. Silicene field-effect transistors operating at room temperature. Nat. Nanotechnol. 2015, 10, 227−231. doi: 10.1038/nnano.2014.325

  28. [28]

      Le Lay, G. Silicene transistors. Nat. Nanotechnol. 2015, 10, 202−203. doi: 10.1038/nnano.2015.10

  29. [29]

      Yang, K.; Cahangirov, S.; Cantarero, A.; Rubio, A.; D'Agosta, R. Thermoelectric properties of atomically thin silicene and germanene nanostructures. Phys. Rev. B 2014, 89, 125403−13. doi: 10.1103/PhysRevB.89.125403

  30. [30]

      Wierzbicki, M.; Barnaś, J.; Swirkowicz, R. Zigzag nanoribbons of two-dimensional silicene-like crystals: magnetic, topological and thermoelectric properties. J. Phys. Condens. Mat. 2015, 27, 485301−14. doi: 10.1088/0953-8984/27/48/485301

  31. [31]

      Jose, D.; Datta, A. Structures and electronic properties of silicene clusters: a promising material for FET and hydrogen storage. Phys. Chem. Chem. Phys. 2011, 13, 7304−7311. doi: 10.1039/c0cp02580a

  32. [32]

      Jinglan, Q.; Huixia, F.; Yang, X.; Oreshkin, A. I.; Tingna, S.; Hui, L.; Sheng, M.; Lan, C.; Kehui, W. Ordered and reversible hydrogenation of silicene. Phys. Rev. Lett. 2015, 114, 126101−126105. doi: 10.1103/PhysRevLett.114.126101

  33. [33]

      Wang, Y.; Rui, Z.; Gao, H.; Jing, Z.; Xu, B.; Qiang, S.; Yu, J. Metal adatoms-decorated silicene as hydrogen storage media. Int. J. Hydrogen Energ. 2014, 39, 14027−14032. doi: 10.1016/j.ijhydene.2014.06.164

  34. [34]

      Xin, T.; Cabrera, C. R.; Chen, Z. Metallic BSi₃ silicene: a promising high capacity anode material for lithium-ion batteries. J. Phys. Chem. C 2014, 118, 25836−25843. doi: 10.1021/jp503597n

  35. [35]

      Hwang, Y.; Yun, K. H.; Chung, Y. C. Carbon-free and two-dimensional cathode structure based on silicene for lithium-oxygen batteries: a first-principles calculation. J. Power Sources 2015, 275, 32−37. doi: 10.1016/j.jpowsour.2014.11.016

  36. [36]

      Rugeramigabo, E. P.; Nagao, T.; Pfnür, H. Experimental investigation of two-dimensional plasmons in a DySi₂ monolayer on Si(111). Phys. Rev. B 2008, 78, 155402−6. doi: 10.1103/PhysRevB.78.155402

  37. [37]

      Yang, L. M.; Bačić, V.; Popov, I. A.; Boldyrev, A. I.; Heine, T.; Frauenheim, T.; Ganz, E. Two-dimensional Cu₂Si monolayer with planar hexacoordinate copper and silicon bonding. J. Am. Chem. Soc. 2015, 137, 2757−2762. doi: 10.1021/ja513209c

  38. [38]

      Yang, L. M.; Popov, I. A.; Boldyrev, A. I.; Heine, T.; Frauenheim, T.; Ganz, E. Post-anti-van't Hoff-Le Bel motif in atomically thin germanium-copper alloy film. Phys. Chem. Chem. Phys. 2015, 17, 17545−17551. doi: 10.1039/C5CP02827B

  39. [39]

      Yang, L. M.; Popov, I. A.; Frauenheim, T.; Boldyrev, A. I.; Heine, T.; Bačić, V.; Ganz, E. Revealing unusual chemical bonding in planar hyper-coordinate Ni₂Ge and quasi-planar Ni₂Si two-dimensional crystals. Phys. Chem. Chem. Phys. 2015, 17, 26043−26048. doi: 10.1039/C5CP04893A

  40. [40]

      Feng, B.; Fu, B.; Kasamatsu, S.; Ito, S.; Cheng, P.; Liu, C. C.; Feng, Y.; Wu, S.; Mahatha, S. K.; Sheverdyaeva, P.; Moras, P.; Arita, M.; Sugino, O.; Chiang, T. C.; Shimada, K.; Miyamoto, K.; Okuda, T.; Wu, K.; Chen, L.; Yao, Y.; Matsuda, I. Experimental realization of two-dimensional Dirac nodal line fermions in monolayer Cu₂Si. Nat. Commun. 2017, 8, 1007−6. doi: 10.1038/s41467-017-01108-z

  41. [41]

      Sun, Y.; Zhuo, Z.; Wu, X.; Yang, J. Room-temperature ferromagnetism in two-dimensional Fe₂Si nanosheet with enhanced spin-polarization ratio. Nano. Lett. 2017, 17, 2771−2777. doi: 10.1021/acs.nanolett.6b04884

  42. [42]

      Wang, Y.; Qiao, M.; Li, Y.; Chen, Z. A two-dimensional CaSi monolayer with quasi-planar pentacoordinate silicon. Nanoscale Horiz. 2018, 3, 327−334. doi: 10.1039/C7NH00091J

  43. [43]

      Exner, K.; Schleyer, P. V. R. Planar hexacoordinate carbon: a viable possibility. Science 2000, 290, 1937−1940. doi: 10.1126/science.290.5498.1937

  44. [44]

      Wen, C.; Xie, Q.; Xiong, R.; Sa, B.; Miao, N.; Zhou, J.; Wu, B.; Sun, Z. Computational mining of the pressure effect on thermodynamic and thermoelectric properties of cubic Ca₂Si. EPL 2018, 123, 67003−6. doi: 10.1209/0295-5075/123/67003

  45. [45]

      Xiong, R.; Sa, B.; Miao, N.; Li, Y. L.; Zhou, J.; Pan, Y.; Wen, C.; Wu, B.; Sun, Z. Structural stability and thermoelectric property optimization of Ca₂Si. RSC Adv. 2017, 7, 8936−8943. doi: 10.1039/C6RA28125G

  46. [46]

      Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251−14269. doi: 10.1103/PhysRevB.49.14251

  47. [47]

      Hafner, J. Ab-initio simulations of materials using VASP: density-functional theory and beyond. J. Comput. Chem. 2008, 29, 2044−2078. doi: 10.1002/jcc.21057

  48. [48]

      Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169−11186. doi: 10.1103/PhysRevB.54.11169

  49. [49]

      Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758−1775.

  50. [50]

      Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953−17979. doi: 10.1103/PhysRevB.50.17953

  51. [51]

      Perdew, J. P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244−13249. doi: 10.1103/PhysRevB.45.13244

  52. [52]

      Perdew, J. P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865−3868. doi: 10.1103/PhysRevLett.77.3865

  53. [53]

      Perdew, J. P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533−16539. doi: 10.1103/PhysRevB.54.16533

  54. [54]

      Monkhorst, H. J.; Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188−5192. doi: 10.1103/PhysRevB.13.5188

  55. [55]

      Heyd, J.; Scuseria, G. E. Efficient hybrid density functional calculations in solids: assessment of the Heyd-Scuseria-Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 2004, 121, 1187−1192. doi: 10.1063/1.1760074

  56. [56]

      Poater, J.; Duran, M.; Sola, M.; Silvi, B. Theoretical evaluation of electron delocalization in aromatic molecules by means of atoms in molecules (AIM) and electron localization function (ELF) topological approaches. Chem. Rev. 2005, 105, 3911−3947. doi: 10.1021/cr030085x

  57. [57]

      Becke, A. D.; Edgecombe, K. E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397−5403. doi: 10.1063/1.458517

  58. [58]

      Maintz, S.; Deringer, V. L.; Tchougréeff, A. L.; Dronskowski, R. Analytic projection from plane-wave and PAW wavefunctions and application to chemical-bonding analysis in solids. J. Comput. Chem. 2013, 34, 2557−2567. doi: 10.1002/jcc.23424

  59. [59]

      Wang, Y.; Chen, L. Q.; Liu, Z. K. YPHON: a package for calculating phonons of polar materials. Comput. Phys. Commun. 2014, 185, 2950−2968. doi: 10.1016/j.cpc.2014.06.023

  60. [60]

      Bardeen, J.; Shockley, W. S. Deformation potentials and mobilities in non-polar crystals. Phys. Rev. 1950, 80, 72−80. doi: 10.1103/PhysRev.80.72

  61. [61]

      Kou, L. Z.; Ma, Y. D.; Zhou, L. J.; Sun, Z. Q.; Gu, Y. T.; Du, A. J.; Smith, S.; Chen, C. F. High-mobility anisotropic transport in few-layer gamma-B-28 films. Nanoscale 2016, 8, 20111−20117. doi: 10.1039/C6NR07271B

  62. [62]

      Jun, D.; Cheng, Z. X. Titanium trisulfide monolayer: theoretical prediction of a new direct-gap semiconductor with high and anisotropic carrier mobility. Angew. Chem. Int. Edit. 2015, 54, 7572−7576. doi: 10.1002/anie.201502107

  63. [63]

      Deringer, V. L.; Zhang, W.; Rausch, P.; Mazzarello, R.; Dronskowski, R.; Wuttig, M. A chemical link between Ge-Sb-Te and In-Sb-Te phase-change materials. J. Mater. Chem. C 2015, 3, 9519−9523. doi: 10.1039/C5TC02314A

  64. [64]

      Deringer, V. L.; Tchougréeff, A. L.; Dronskowski, R. Crystal orbital hamilton population (COHP) analysis as projected from plane-wave basis sets. J. Phys. Chem. A 2011, 115, 5461−5466. doi: 10.1021/jp202489s

  65. [65]

      Qiao, J.; Kong, X.; Hu, Z. X.; Yang, F.; Ji, W. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 2014, 5, 4475−7. doi: 10.1038/ncomms5475

  66. [66]

      Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS₂ transistors. Nat. Nanotechnol. 2011, 6, 147−150. doi: 10.1038/nnano.2010.279

• 

  Figure 1  (a) Side and top views of the optimized structure of 2D Ca₂Si monolayer. (b) ELF profile on the (110) plane of Ca₂Si monolayer. The interval between the contour lines is 0.16. (c) The calculated COHP of Ca–Si and Ca–Ca bonds in Ca₂Si monolayer. The inset of Fig. 1c is the 3D ELF profile of Ca₂Si monolayer

  下载: 全尺寸图片 幻灯片
  

  Figure 2  Evolution of total energy and snapshots from AIMD simulations at 0 and 10 ps at (a) 300 K, (b) 600 K, (c) 900 K, (d) 1200 K and (e) 1500 K of Ca₂Si monolayer. (f) Phonon dispersion curve of Ca₂Si monolayer under ambient condition using PBE functional

  下载: 全尺寸图片 幻灯片
  

  Figure 3  Projected energy band structure of Ca₂Si monolayer by (a) GGA–PBE and (b) HSE06 hybrid functional methods. The red and blue solid lines represent the projected specific gravity of Si electrons and Ca electrons, respectively. The fermi level is set to E = 0.0 eV

  下载: 全尺寸图片 幻灯片
  

  Figure 4  (a) Using an orthorhombic lattice instead of a traditional hexagonal lattice to calculate Ca₂Si monolayer and the transformed Ca₂Si monolayer Brillouin zone. (b) Band structure of Ca₂Si monolayer by PBE. (c) Total energy shift E – E₀ and (d) Band edge positions of Ca₂Si monolayer as a function of the uniaxial strain ε along both the zigzag (x) and armchair (y) directions by PBE. The vacuum level is set to 0 for reference in (d) figure

  下载: 全尺寸图片 幻灯片
  

  Figure 5  Carrier mobility of electrons and holes as a function of directions for Ca₂Si monolayer

  下载: 全尺寸图片 幻灯片

  Table 1.  Calculated Effective Mass (m*), Elastic Modulus C_2D, Deformation Potential Constant E_i, and Carrier Mobilityμ for Electrons and Holes along Both the Zigzag (x) and Armchair (y) Directions at 300 K in Ca₂Si Monolayer

  Carrier type	m*·m0–1	C2D (N·m–1)	|Ei| (eV)	μ (cm2·V–1·s–1)
  Electron (x)	1.064	31.99	0.465	1894.92
  Hole (x)	1.105	31.99	4.144	22.13
  Electron (y)	0.986	31.92	0.322	4590.47
  Hole (y)	28.902	31.92	1.518	0.24

  下载: 导出CSV
•